ヘロンの公式を証明 三角形の三辺さえ分かっていれば面積が求まるという、非常に面白いヘロンの公式ですが、 「なぜ、ヘロンの公式は成り立つのでしょうか?」 最後に、ヘロンの公式を証明してみましょう。 次の三角形を考えます。ヘロンの公式 計算機 留意事項 入力値は、整数・分数・小数のいずれか、当然ですが正の値に限ります。 入力可能文字数(桁数ではありません)は、最大7文字です。 (「12/5」は4文字、「」は6文字とカウントされます) 分数の入力書式 「1/2」(2ヘロンの公式(ヘロンのこうしき、英 Heron's formula )とは、3辺の長さが a, b, c などと分かっている三角形の面積 S を求める公式のことである。 アレクサンドリアのヘロン が彼の著書『 Metrica 』の中で証明を与えていることから彼に帰せられる 1 。

ヘロンの公式 三角形の面積を求める 数学のカ
ヘロンの公式 証明
ヘロンの公式 証明-この証明は次のように行います。 ABCの面積は ですが、ahをa,b,cだけの式に直すと、ヘロンの公式となります。 図で、h 2 =c 2x 2 =b 2(ax) 2 、従って c 2x 2 =b 2a 2 2axx 2MathAquarium定理・公式の証明三角形の面積(ヘロンの公式) 1 三角形の面積 ABC において,頂点A,B,C における角の大きさ をA,B,C,その対辺BC,CA,AB の長さをそれぞれ a,b,c,面積をS とすると,次の等式が成り立つ。 S= 2 1 bc sinA= 2 1 ca sinB= 2 1 ab
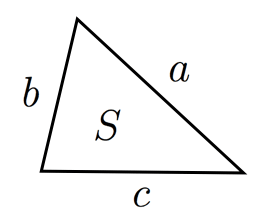


ヘロンの公式の証明と使用例 高校数学の美しい物語
ヘロンの公式の証明 次にヘロンの公式を証明します。 ただ、「ヘロンの公式を証明せよ」といった問題はほとんど出題されないので覚えなくてもいいという人は飛ばしてしまっても構いません。 大事なのは計算問題です。 この公式の証明方法はいろいろありますが、ここでは一番シンプルなものを紹介します。 方針は「 sinを使った面積の公式から上手く式変形(ヘロンの公式の証明の途中式(※)のルートの中身を整理することで得られます。 例題3 三辺の長さが 5 , 7 , 3 \sqrt{5},\sqrt{7},3 5 , 7 , 3 であるような三角形の面積を求めよ。ヘロンの公式の証明 ヘロンの公式の証明には、 内接円の性質を利用した証明 と 三角関数を用いた証明 があります。 証明は少しむずかしいですが、証明方法を知ることでより理解が深まり、他の問題を解くときの手がかりにもなります。
ヘロンの公式の証明 辺の長さが である2辺の間の角を とします。 三角比を用いた三角形の面積より、 (1) 余弦定理より、 (2) 三角比の相互関係式より、 (3) (2)式を(3)式に代入すると、ヘロンの公式についての質問です。 ひとつ前の赤チャートのヘロンの公式の証明で bc sin A=bc√1cos^2 A=√b^2c^2(1cosA)(1cosA) と、ここまではokなのですが、 その後 2bc(1cosA)=(bca)(bca) 2bc(1co概要 ブラーマグプタの公式は、7世紀にインドの数学者 ブラーマグプタがヘロンの公式の一般化として得た定理である。 ヘロンの公式は三角形の3辺の長さから三角形の面積を求める公式であるが、ブラーマグプタの公式は四角形の 4辺の長さから四角形の面積を求める公式である。
と、証明できました 中学数学の知識で証明する 中学数学では、三角関数や余弦定理について学ばないので、これらを使わずに証明していきます 三角形abcの頂点aから線分bcに垂線を下ろし、交点をhとします ah = h , bh = dとおきますヘロンの公式は、三角形の3辺の長さから面積を求めるための公式です。 なぜ3辺の長さから面積が求められるのでしょうか? そもそも三角形の面積は「底辺 × 高さ ÷ 2」なので、高さがわからなければ面積もわからないのこの点について、ヘロンの公式を高校2年のときに学んで以来、ヘロンの公式を目にする 度に幾ばくかの違和感を感じていた。 ところが、ブラマグプタの公式を用いれば、この違和感は一掃される。s の存在にも必然 性があったのだ!



高校数学 三角形の外接円の半径 内接円の半径と面積の関係 S 1 2r A B C 受験の月



ヘロンの公式の幾何的証明 怜悧玲瓏 高校数学を天空から俯瞰する
ヘロンの公式(幾何的証明)代数的証明はこちら 三角形の三辺の長さ a,b,c が分かっているとき、三角形の面積Sは、 とヘロンの公式(幾何的証明)代数的証明はこちら 三角形の三辺の長さ a,b,c が分かっているとき、三角形の面積Sは、 とヘロンの公式とは。 図解でわかるその仕組みと証明方法 Tooda Yuuto 18年10月13日 / 年3月6日 ヘロンの公式とは、三角形の3辺の長さ a, b, c を使って素早く三角形の面積を求める公式です。 3辺の長さが a, b, c の三角形の面積 S は S = s ( s − a) ( s − b) ( s − c) ただし、 ( た だ し 、 s = a b c 2) で求められる



三辺の長さが与えられた三角形の面積を求めるヘロンの公式の別証明 身勝手な主張



ヘロンの公式とは ヘロンの公式の証明と使い方 演習問題付き Himokuri
ヘロンの公式の証明(三角関数を使わずに) ヘロンの公式 は任意の 三角形 の3辺 a , b , c の長さから 面積S を求める 公式である 。 アレクサンドリアのヘロン が彼の著書『 Metrica 』の中で証明を与えていることから彼に帰せられる。ヘロンの公式の証明(三角関数を使わずに) ヘロンの公式 は任意の 三角形 の3辺 a , b , c の長さから 面積S を求める公式である。 アレクサンドリアのヘロンが彼の著書『Metrica』の中で証明を与えていることから彼に帰せられる。 この証明には三角関数が多く用いられるが,中学校の内容で証明をしてみることにする。 AからBCに垂線を引き,その垂線の足をDとするキーワード:ヘロンの公式,因数定理,同次多項式,逆問題 1.序 ― 美しいヘロンの公式とは 平面幾何学にヘロン( Heron )の公式という著名な定理がある. これは三角形の 3 辺の長さからその面積を求める大変綺麗な公式である. ABC の角A,
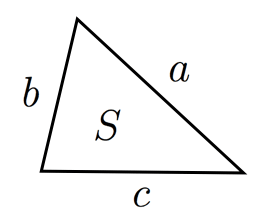


ヘロンの公式の証明と使用例 高校数学の美しい物語


三角関数を使った三角形の面積の求め方とヘロンの公式の証明
/5/13 数Ⅱ:式と証明の全面改訂を完了し、pdfの販売を開始。 /6/22 数Ⅱ:複素数と方程式の全面改訂を完了し、pdfの販売を開始。 /8/19 数Ⅱ:三角関数の全面改訂を完了し、pdfの販売を開始。 数B:ベクトルのpdfに空間の方程式を追加。ヘロンの公式は、高校1年生で学習する余弦定理を用いることで、証明することができます。 3辺の長さ a, b, c の ABC の面積を S として、これを求めましょう。(再追記) 例6.において、ヘロンの公式の初等的証明を示したが、次のような証明がある ことを最近知った。 ヘロンの公式における s-a、s-b、s-c の意味が分かって、思わず唸って しまった。



ヘロンの公式とは ヘロンノコウシキとは 単語記事 ニコニコ大百科
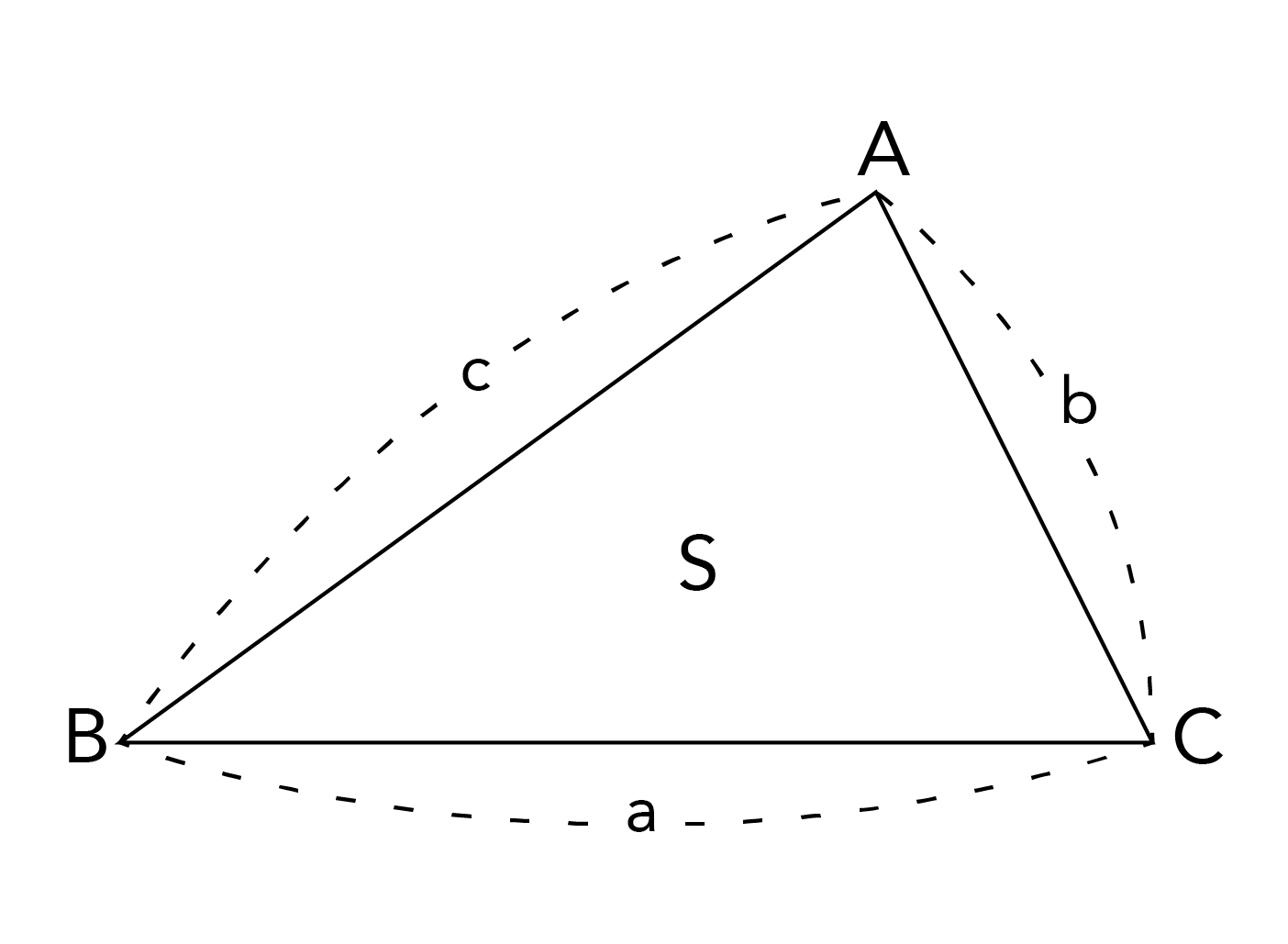


ヘロンの公式が一目でわかる 見やすい図で慶應生が解説 高校生向け受験応援メディア 受験のミカタ
この公式を用いて、ヘロンの公式を証明します。 まず、余弦定理により、 $$\cos{A}=\frac{b^2c^2a^2}{2bc}$$ となります。 余弦定理については、下の記事に詳しくまとめています。3辺の長さから三角形の面積を求める公式です。 中学生から高校生まで、知っていると非常に便利な計算方法です。 ①ヘロンの公式と名前の由来 ②証明(中3レベル) ③証明(数Ⅰレベル) ①ヘロンの公式と中学数学 数学 高校数学 中学数学で出来る! ヘロンの公式の証明 21年2月3日 ヘロンの公式は、三角形の3辺の長さから面積を求める公式です 以下の三角形ABCの面積Sは S = s ( s − a) ( s − b) ( s − c) ( s = a b c 2) 今回は、この公式の「三角関数を使って
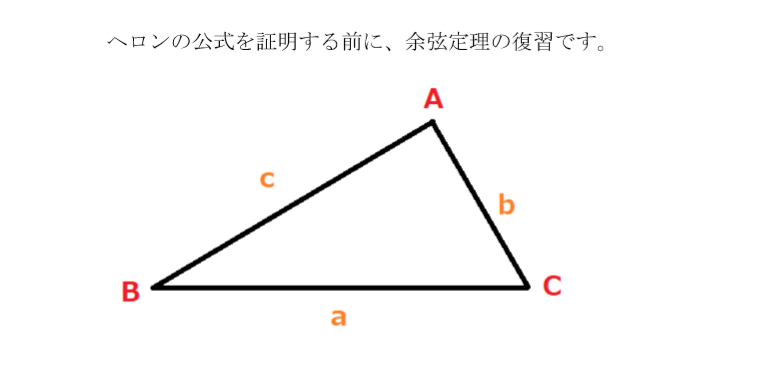


ヘロンの公式 三角形の3辺の長さから面積を求める公式 いまあつ予報士のブログ


011 7 49 大学受験完全個別指導予備校 実力養成会 The Ability Training School 実力養成会について 学習システム 費用 ニュース ブログ 実力養成会を選んだ理由 実力養成会の考え方 講師紹介 実績 よくあるご質問 ニュース ブログ ホーム ニュース
ヘロンの公式を三平方の定理から導く ヘロンの公式 3辺の長さがa,b,cであるような ABCの面積Sは、2t=abcとおくと、次式で求まる。この公式を用いて、ヘロンの公式を証明します。 まず、余弦定理により、 $$\cos{A}=\frac{b^2c^2a^2}{2bc}$$ となります。 余弦定理については、下の記事に詳しくまとめています。前回 https//wwwyoutubecom/watch?v=6MBwzRYm4&index=18&list=PLKRhhk0lEyzOfDE8u9U0GWX3aa43XeMOr 次回 https//wwwyoutubecom/watch?v=cSbY6lb4fng&index



100 ヘロン の 公式 中学 人気のある画像を投稿する


ヘロンの公式 京極一樹の数学塾
ヘロンの公式の証明 ではこの公式を証明していきましょう。 ABCにおいて、 余弦定理 より"a²=b²+c²−2b・c・cosA"なので ー① 続いて sin²A+cosA²=1 "の公式より これに①を代入すると ここで" a+b+c=2s "とすると、 b+c−a=a+b+c−2a=2s−2a=2 (s−a) ー② a−b+c=a+b+c−2b=2s−2b=2 (s−b) ー③


頻出公式証明問題 微積分以外 京極一樹の数学塾
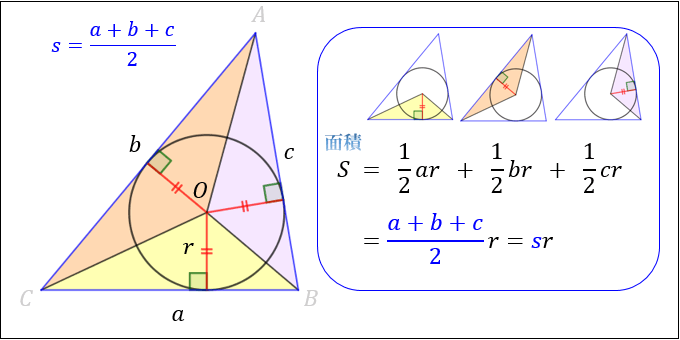


ヘロンの公式とは 図解でわかるその仕組みと証明方法 アタリマエ



Haruka先生の数学証明シリーズ ヘロンの公式 中学レベル Youtube



高校数学 三角比 三角比を使った三角形の面積の求め方 Sin Cos ヘロンの公式を使った方法 数学の面白いこと 役に立つことをまとめたサイト



ヘロンの公式のスモールsってどういう意味でしょうか 誰か教えてくださいm M 基塾長の成績の上がるブログ
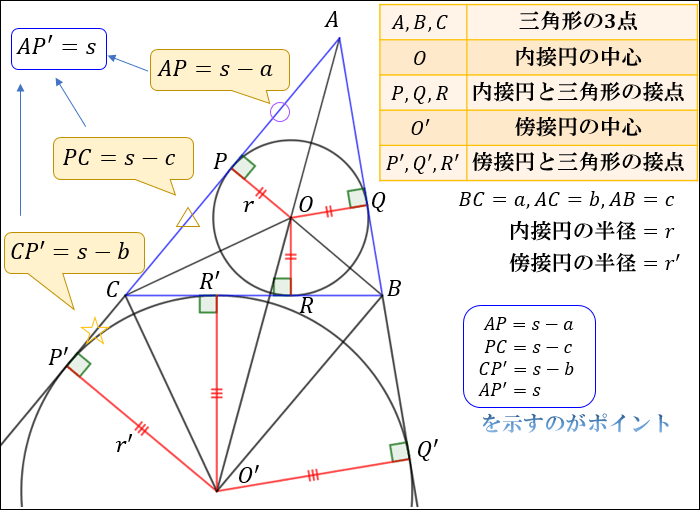


ヘロンの公式とは 図解でわかるその仕組みと証明方法 アタリマエ
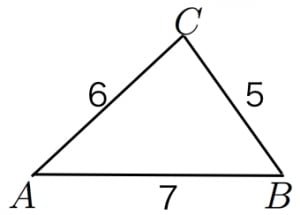


ヘロンの公式の証明と使用例 高校数学の美しい物語



ブラーマグプタの公式 東大合格コム



本には載せなかった第7話 早稲田大学の入試問題より ヘロンの公式の証明 の別解です 花結び


N Y Cityのまちかど Heron S Formula


ヘロンの公式 思考力を鍛える数学


Math Battle 0150 ヘロンの公式の証明


ヘロンの公式の簡単な証明はありますか Quora



ヘロンの公式の幾何的証明 怜悧玲瓏 高校数学を天空から俯瞰する



ヘロンの公式 三角形の面積を求める 数学のカ
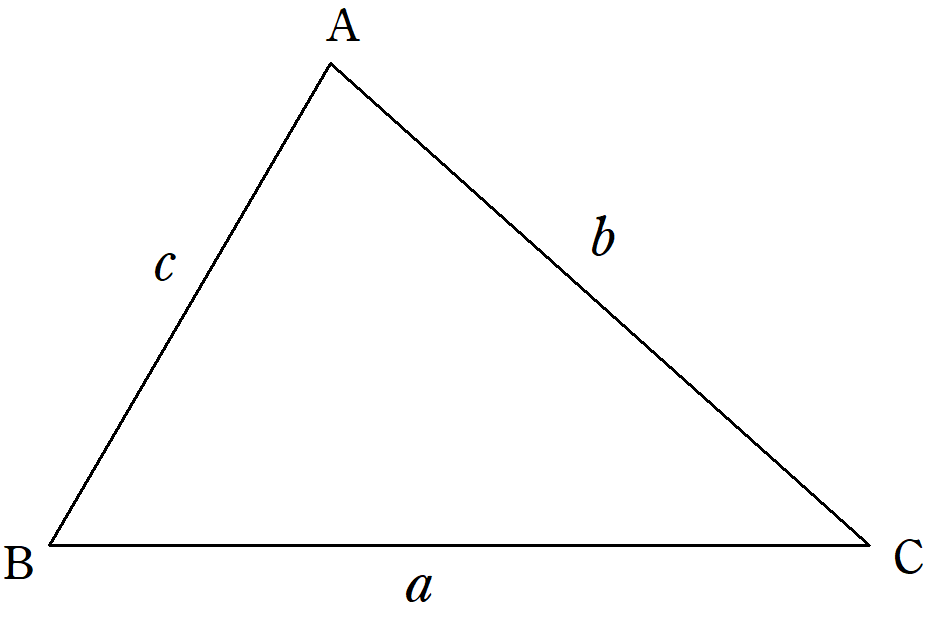


ヘロンの公式 Fukusukeの数学めも


ヘロンの公式の一般化
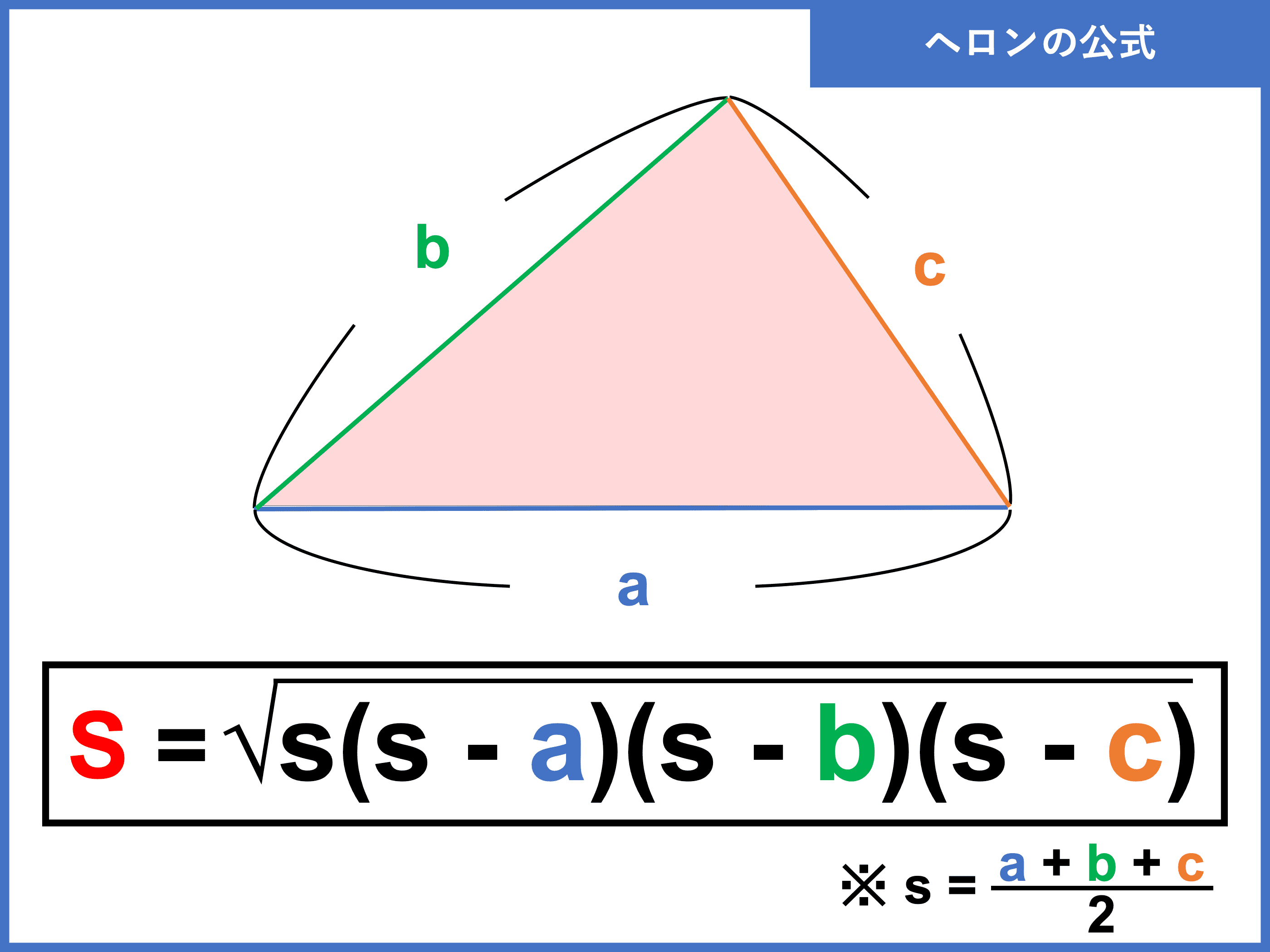


ヘロンの公式とは 証明や 四角形版 ブラーマグプタの公式 も 受験辞典



ヘロンの公式 を使って面積を求める方法 証明あり ますますmathが好きになる 魔法の数学ノート


ヘロンの公式の証明 高校数学マスマスター 学校や塾では教えてくれない 元塾講師の思考回路の公開


三石 数学塾 三角形の面積



ヘロンの公式 計算を工夫して証明 今週の定理 公式no 4 Youtube


ヘロンの公式



三角比35 ヘロンの公式を1分で証明する 怜悧玲瓏 高校数学を天空から俯瞰する



ヘロンの公式
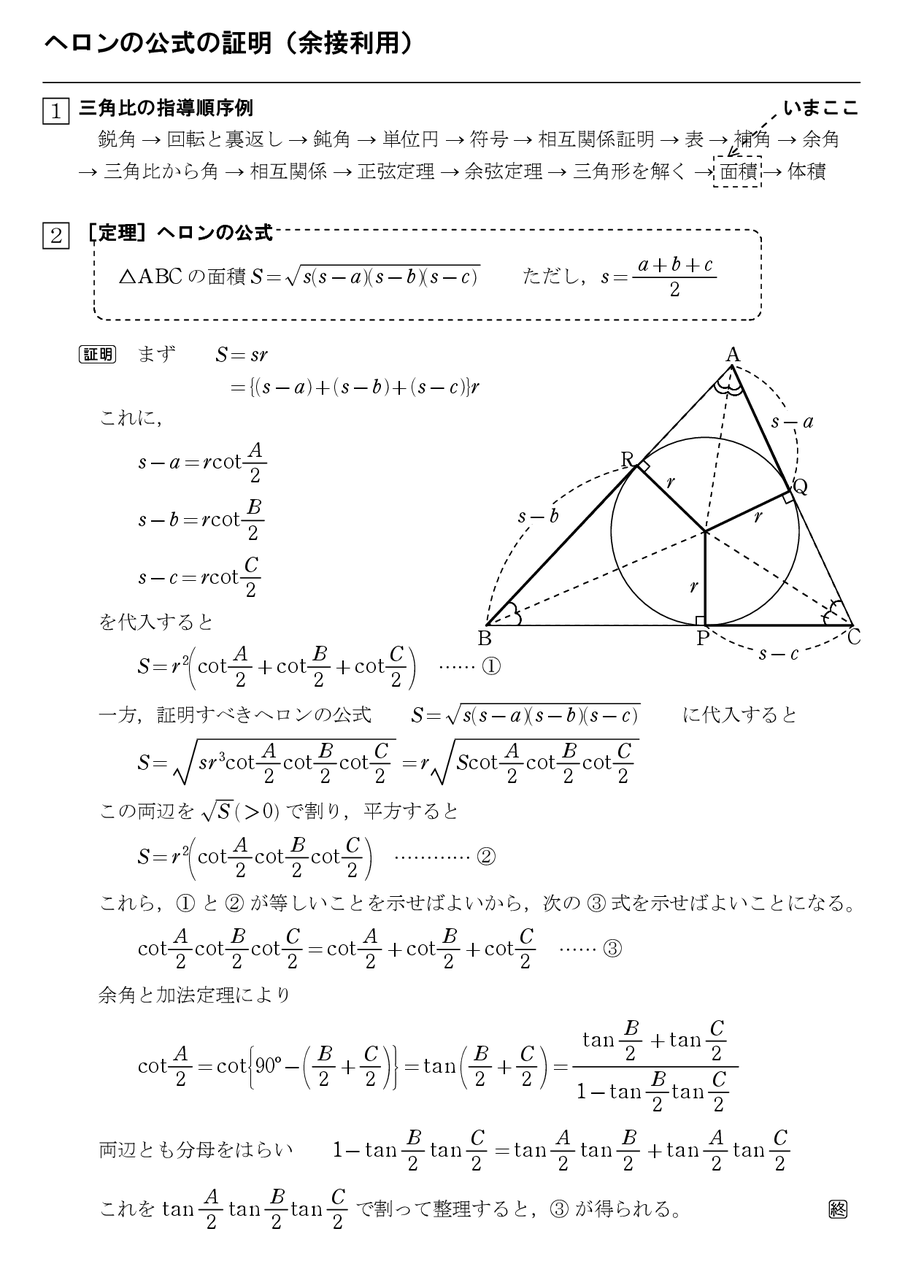


ヘロンの公式の証明 余接利用 怜悧玲瓏 高校数学を天空から俯瞰する



本には載せなかった第7話 早稲田大学の入試問題より ヘロンの公式の証明 の別解です 花結び



ヘロンの公式の証明 余接利用 怜悧玲瓏 高校数学を天空から俯瞰する



三角比38 ヘロンの公式の図形的証明 怜悧玲瓏 高校数学を天空から俯瞰する


ヘロンの公式の2sってなんの略ですか もし略でもなんでもなかったら数学者っ Yahoo 知恵袋



ヘロンの公式 導出と計算例



3分で理解 ヘロンの公式の使い方をイチからていねいに解説 数スタ



3分で分かる ヘロンの公式 証明と問題の解き方をわかりやすく 合格サプリ



ヘロンの公式の証明 ウィキバーシティ


ヘロンの公式の部屋


三平方の定理とヘロン三角形の話
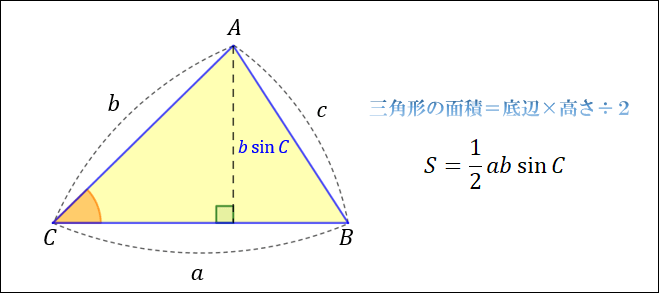


ヘロンの公式とは 図解でわかるその仕組みと証明方法 アタリマエ
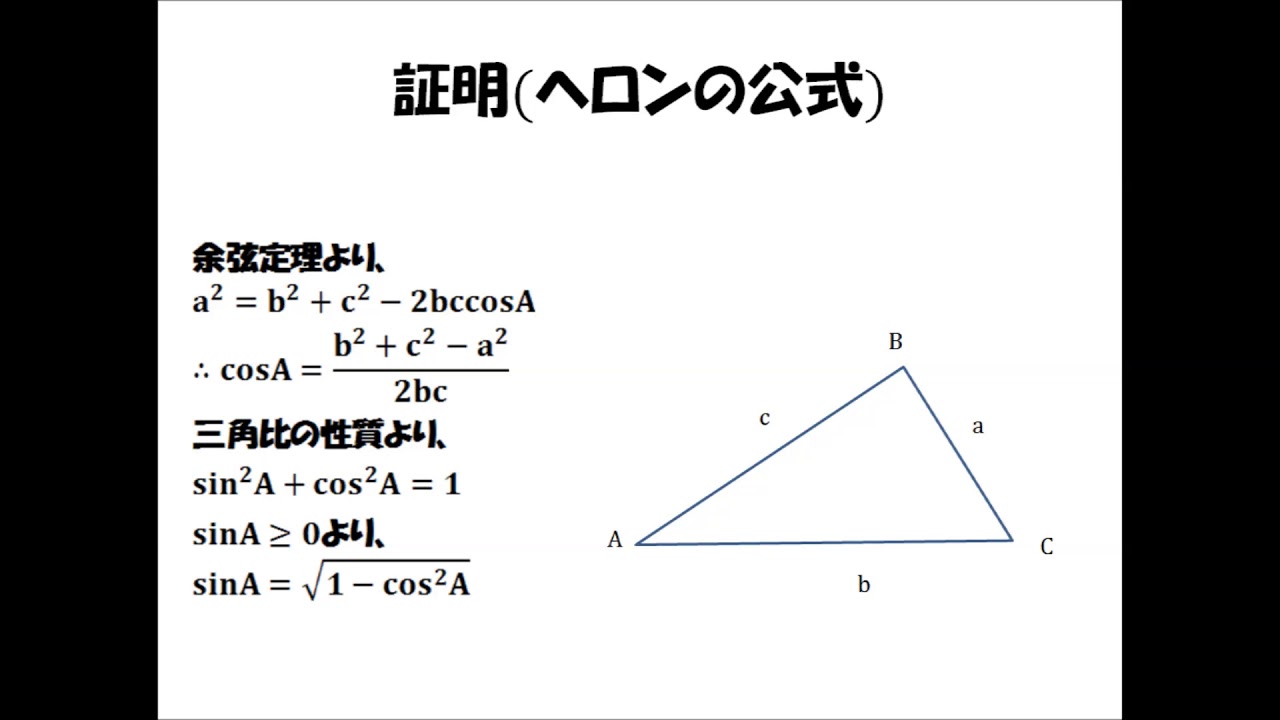


Haruka先生の数学証明シリーズ ヘロンの公式 Youtube
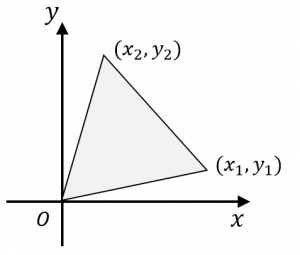


座標平面上で三角形の面積を計算する公式 具体例で学ぶ数学



怜悧玲瓏 高校数学を天空から俯瞰する
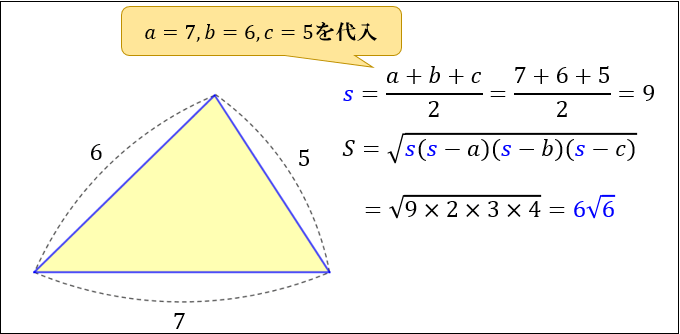


ヘロンの公式とは 図解でわかるその仕組みと証明方法 アタリマエ
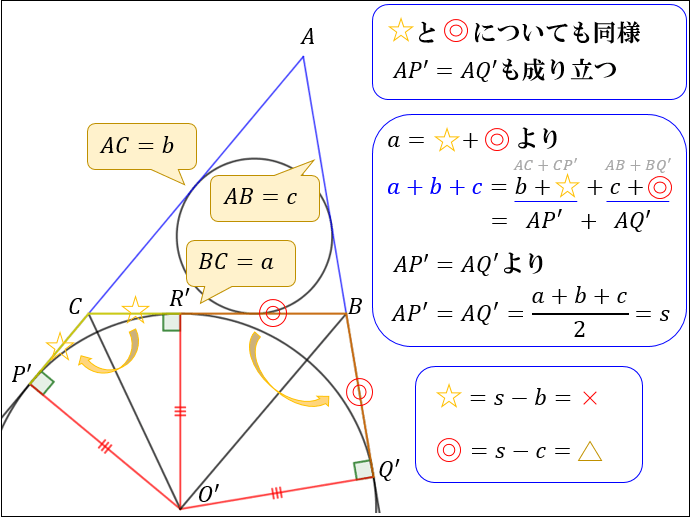


ヘロンの公式とは 図解でわかるその仕組みと証明方法 アタリマエ



三角形の内接円の半径の求め方 公式 練習問題付き 理系ラボ
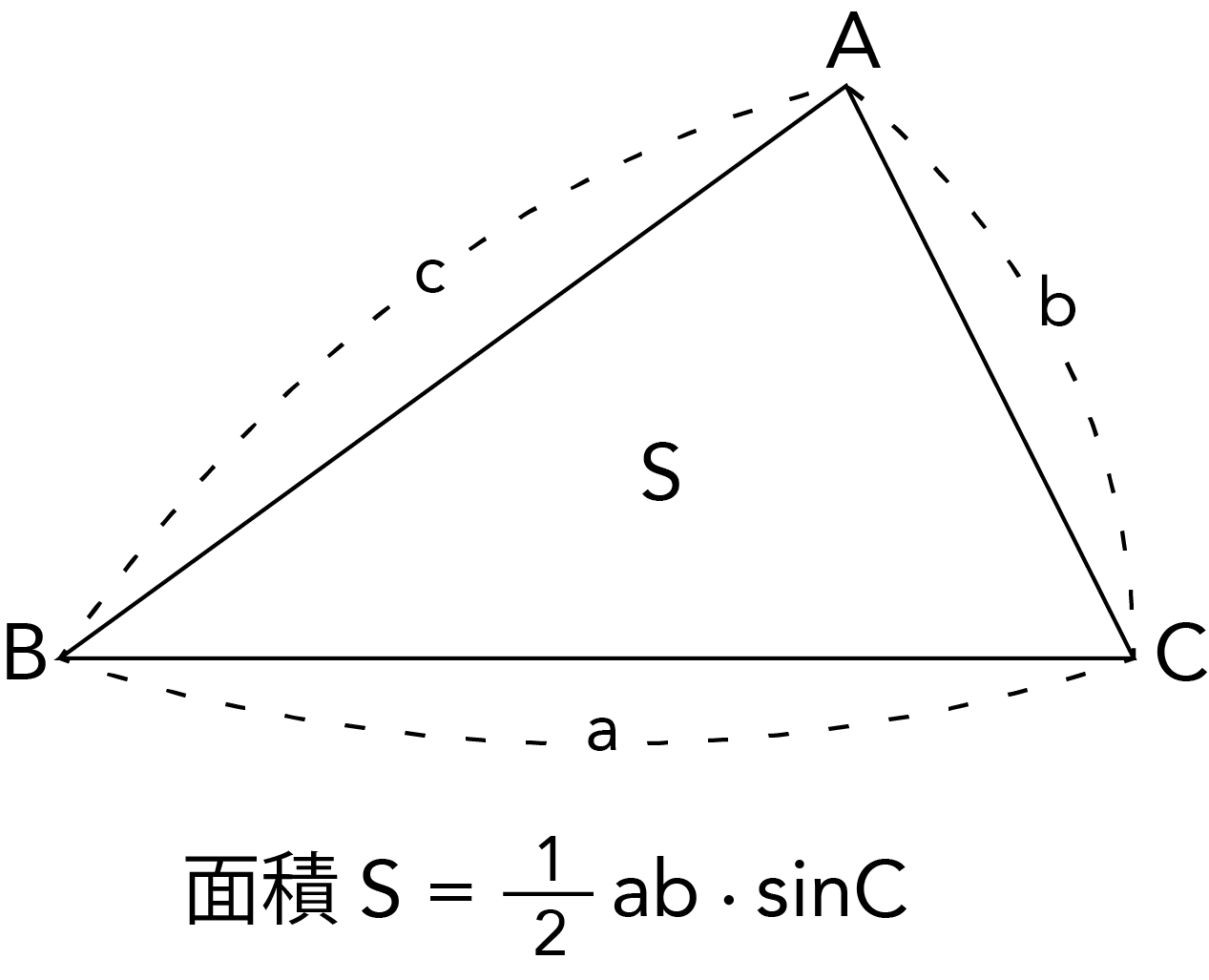


ヘロンの公式が一目でわかる 見やすい図で慶應生が解説 高校生向け受験応援メディア 受験のミカタ


正弦定理の証明



ヘロンの公式のスモールsってどういう意味でしょうか 誰か教えてくださいm M 基塾長の成績の上がるブログ


ヘロンの公式の一般化
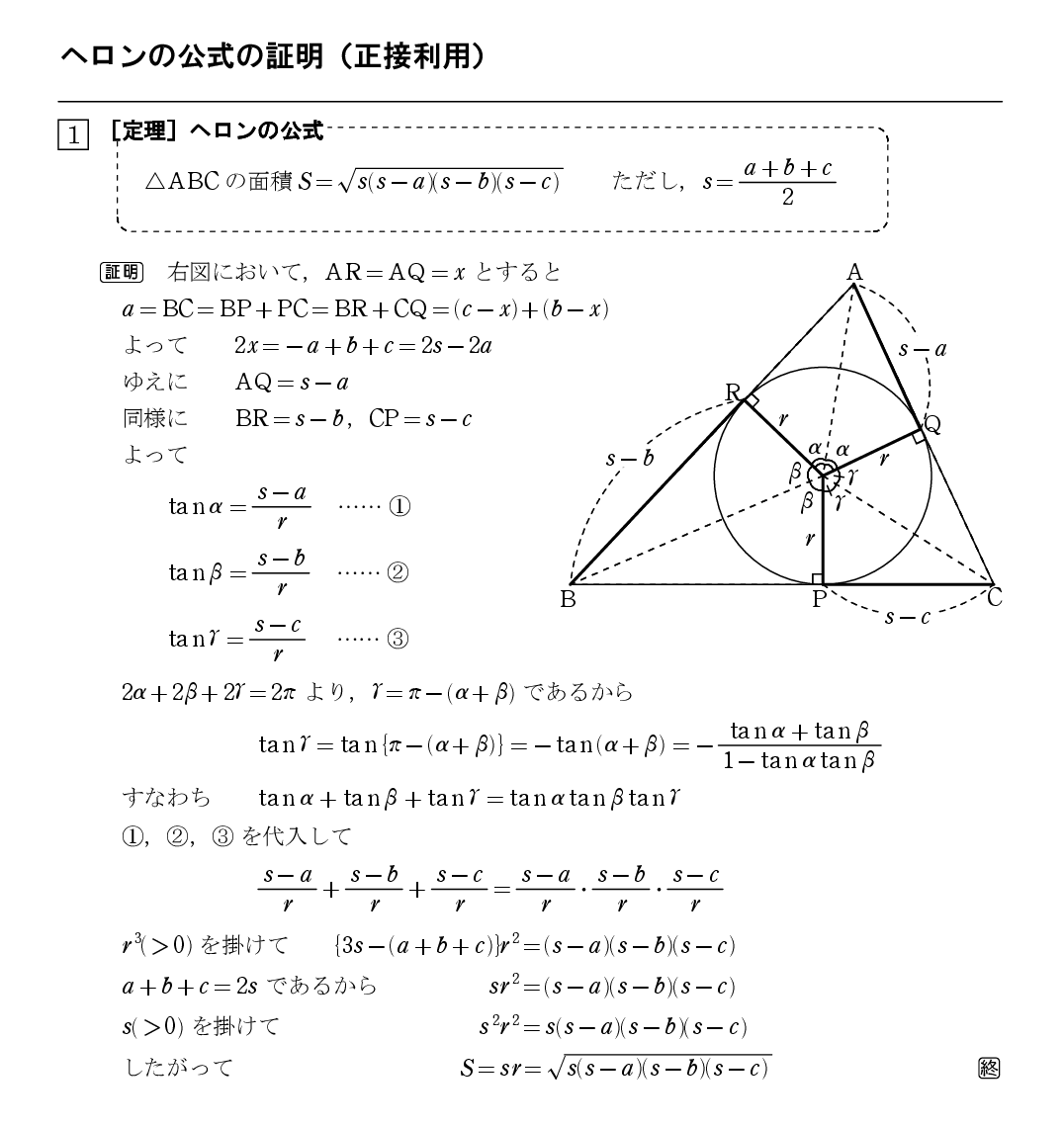


授業での雑談ネタ 18 ヘロンの公式の有名でない証明 怜悧玲瓏 高校数学を天空から俯瞰する


ヘロンの公式の部屋



ヘロンの公式の証明 Youtube



ヘロンの公式 その証明 身勝手な主張



ヘロンの公式とは 図解でわかるその仕組みと証明方法 アタリマエ
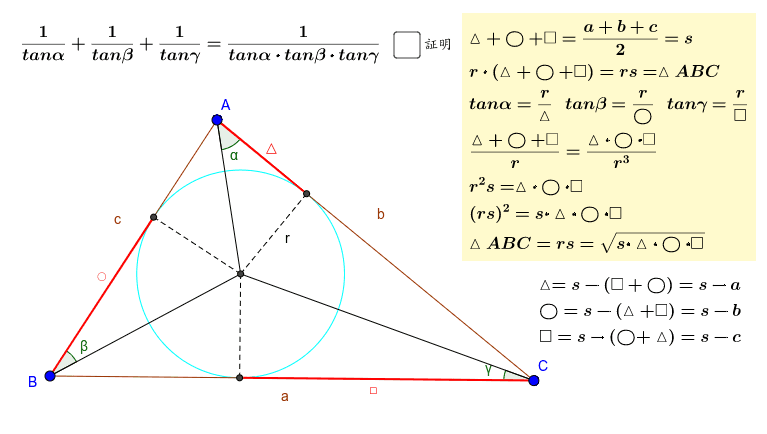


ヘロンの公式 Geogebra
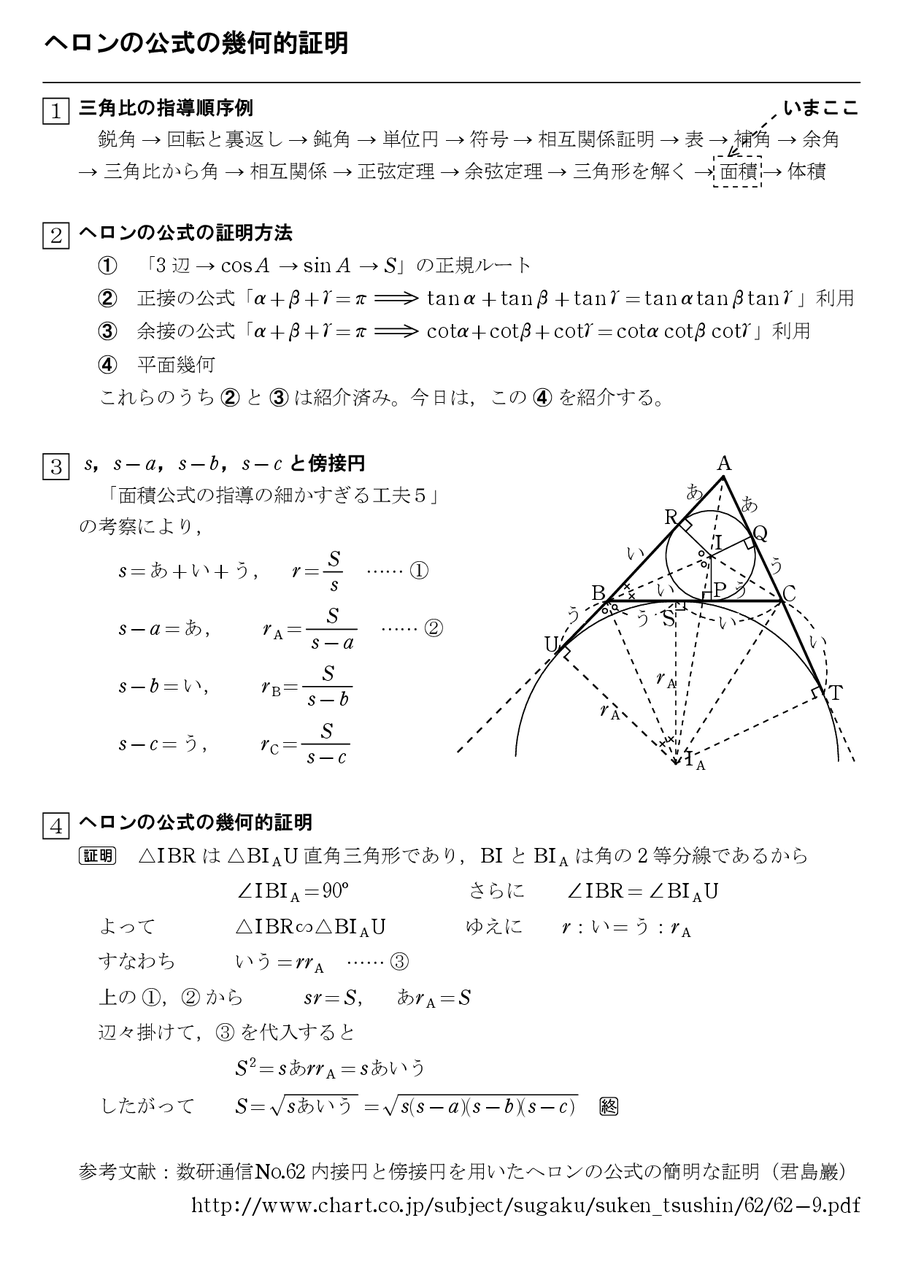


ヘロンの公式の幾何的証明 怜悧玲瓏 高校数学を天空から俯瞰する


N Y Cityのまちかど Heron S Formula



Uzivatel 石松拓人 Na Twitteru ちょっと前に 3辺の和が19の三角形の面積の最大値を求めよ って問題見た気がするんだけど ヘロンの公式を使わずにエレガントな解法思い付いたから見て ってかこれで証明になってる 数学クラスタの人



ヘロンの公式の証明 導出 を徹底解説 5分でわかる Youtube
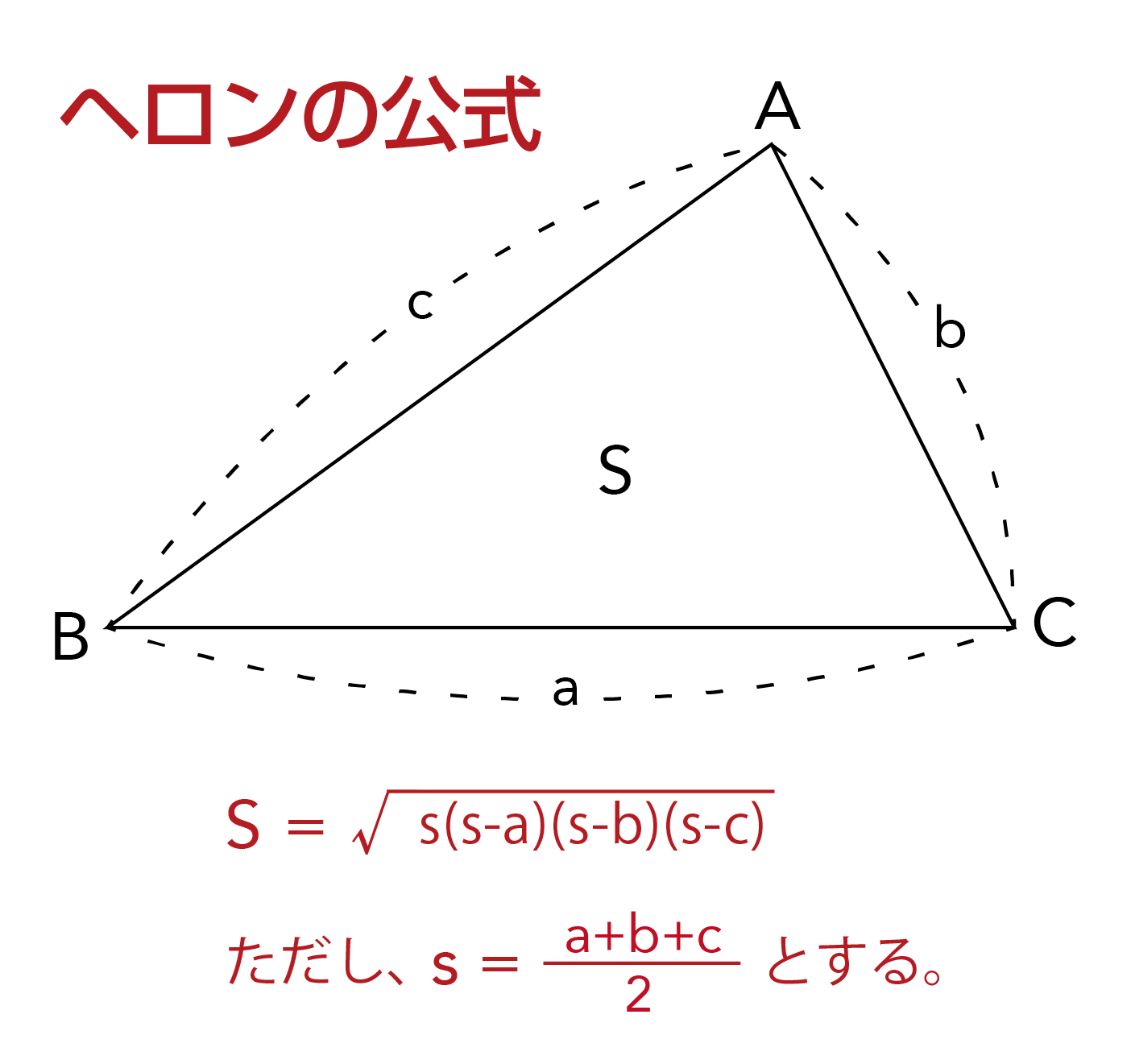


ヘロンの公式が一目でわかる 見やすい図で慶應生が解説 高校生向け受験応援メディア 受験のミカタ



ヘロンの公式で三角形の面積を求める 三辺の長さがわかっているときはコレ 数学の面白いこと 役に立つことをまとめたサイト
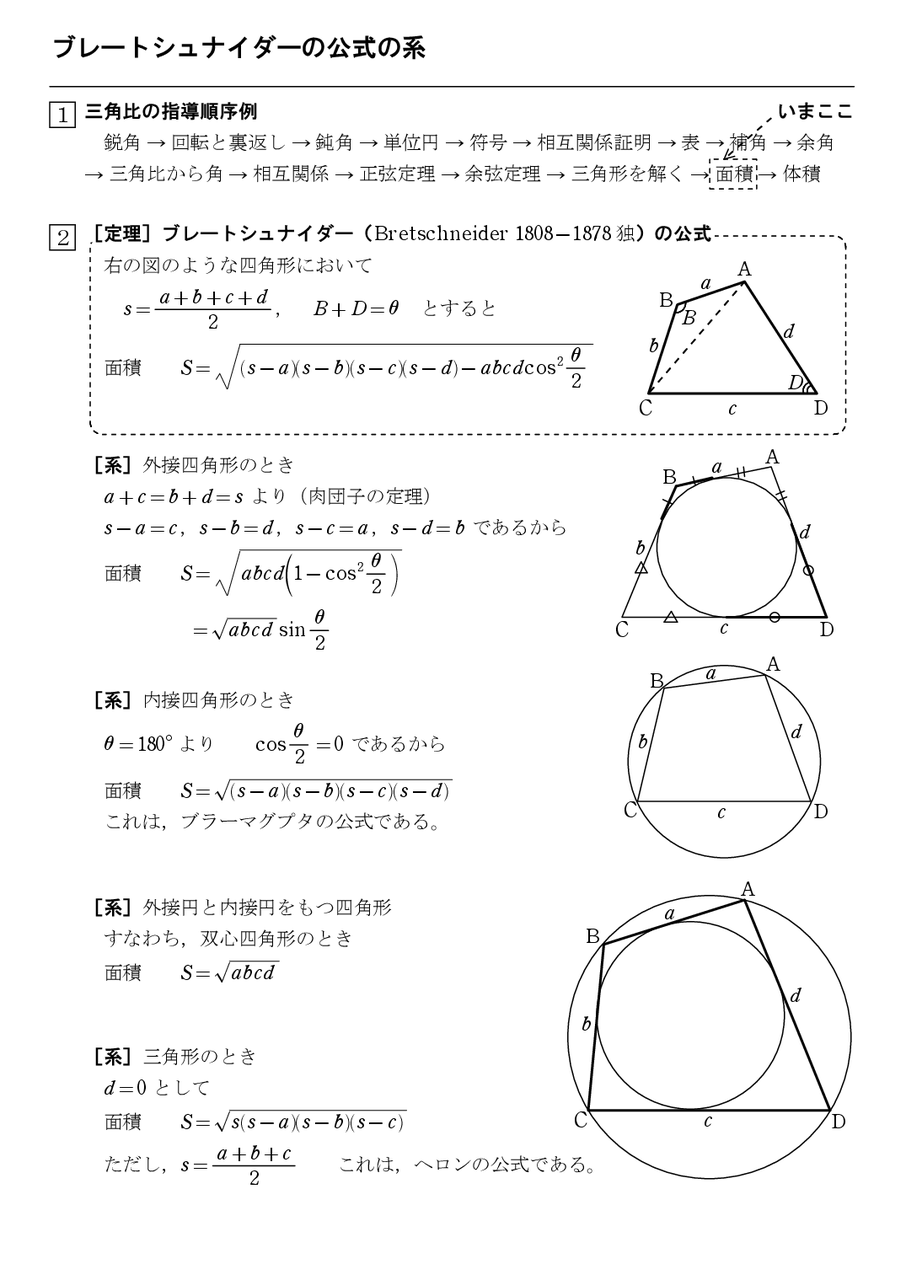


ヘロンの公式の幾何的証明 怜悧玲瓏 高校数学を天空から俯瞰する



高校生 ヘロンの公式のノート一覧 Clear


ヘロンの公式の展開 あっていますか ヘロンの公式を画像の1 2のように2 Yahoo 知恵袋



重心の存在証明とヘロンの公式の証明 大阪教育大学10年後期数学第2問 理系のための備忘録



ヘロンの公式 その証明 身勝手な主張



高校数学 数 94 三角形の面積 ヘロンの公式編 Youtube
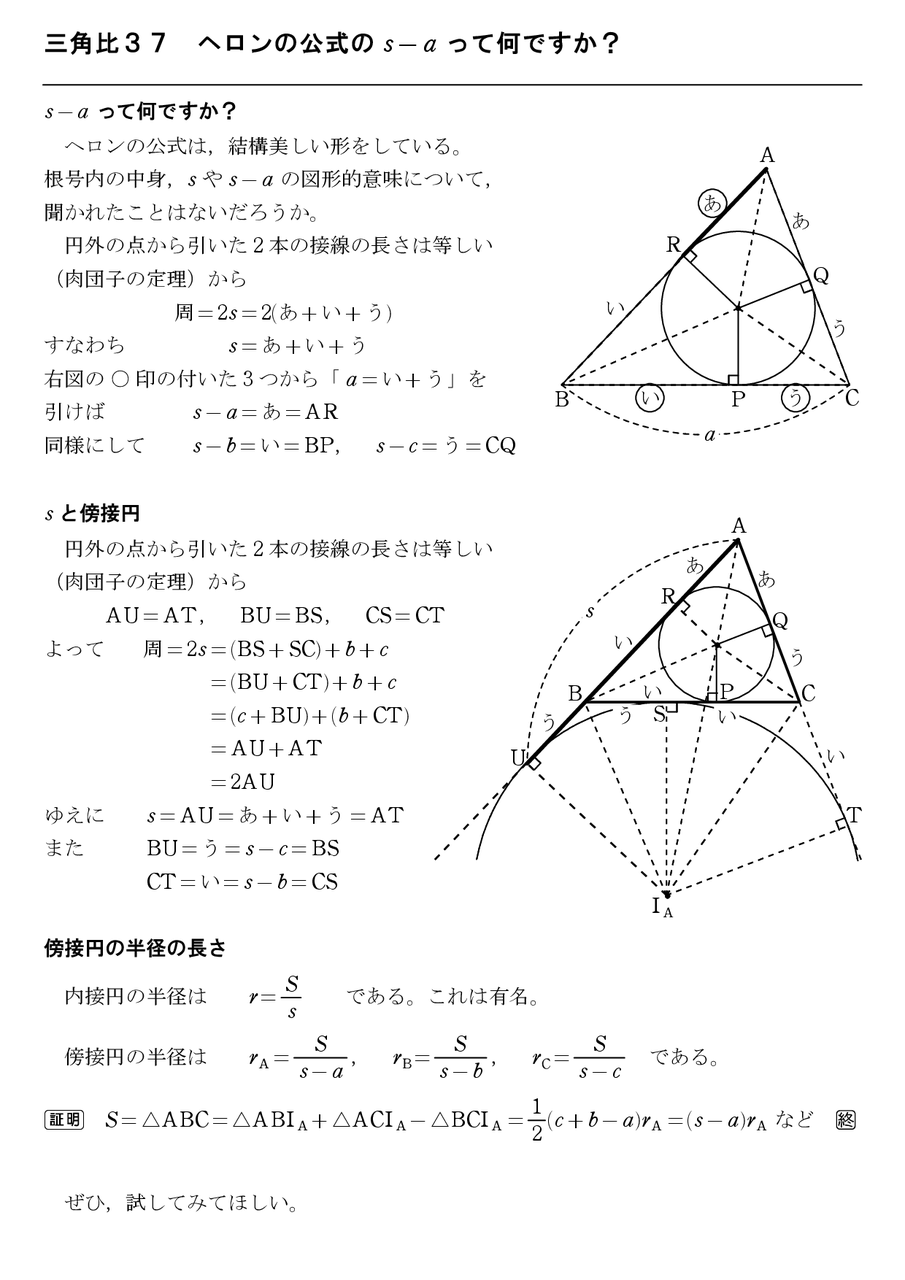


三角比38 ヘロンの公式の図形的証明 怜悧玲瓏 高校数学を天空から俯瞰する



高校数学 三角形の面積のヘロンの公式s S S A S B S C の証明と利用 受験の月



タンジェントの美しい関係式 Tana Tanb Tanc Tanatanbtanc 高校数学の美しい物語


カルダノ



ヘロンの公式 東大合格コム
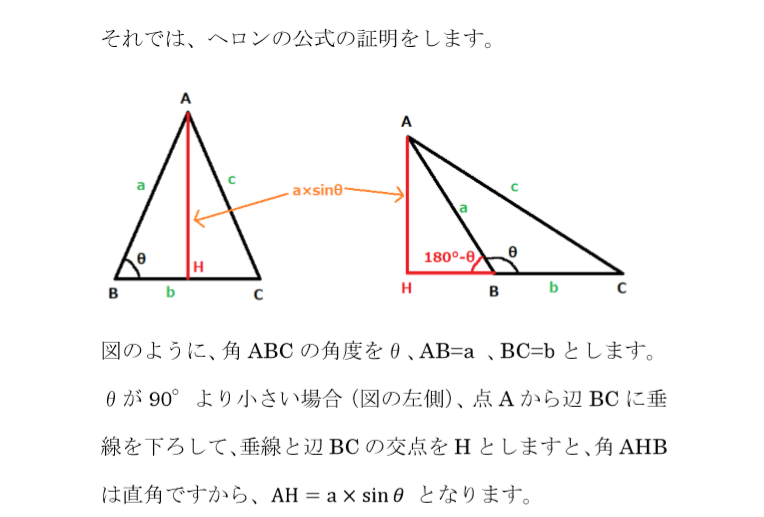


ヘロンの公式 三角形の3辺の長さから面積を求める公式 いまあつ予報士のブログ
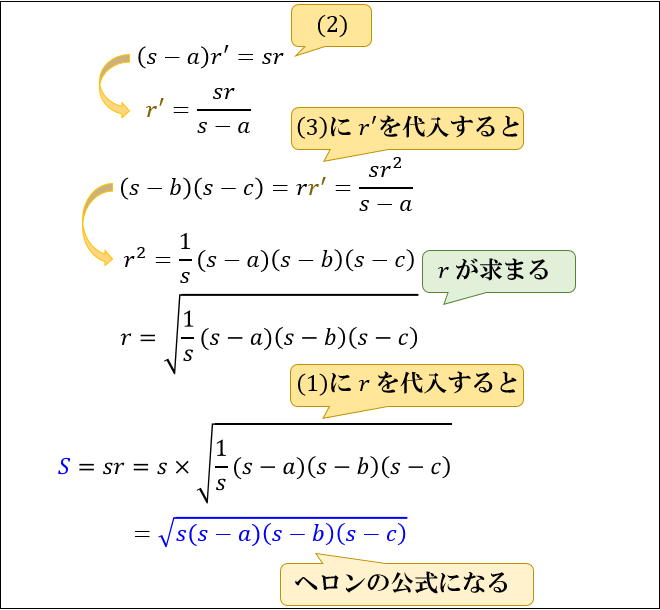


ヘロンの公式とは 図解でわかるその仕組みと証明方法 アタリマエ



三角形の面積を求める公式7選 高校数学のまとめにどうぞ



発展講座 ヘロンの公式とその証明 南数英指導会 南ノートブログ版



ヘロンの公式の幾何的証明 怜悧玲瓏 高校数学を天空から俯瞰する
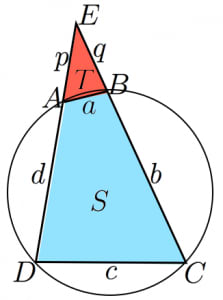


ブラーマグプタの公式とその2通りの証明 高校数学の美しい物語



ヘロンの公式とは 図解でわかるその仕組みと証明方法 アタリマエ



ヘロンの公式 Wikipedia



ヘロンの公式とは 図解でわかるその仕組みと証明方法 アタリマエ
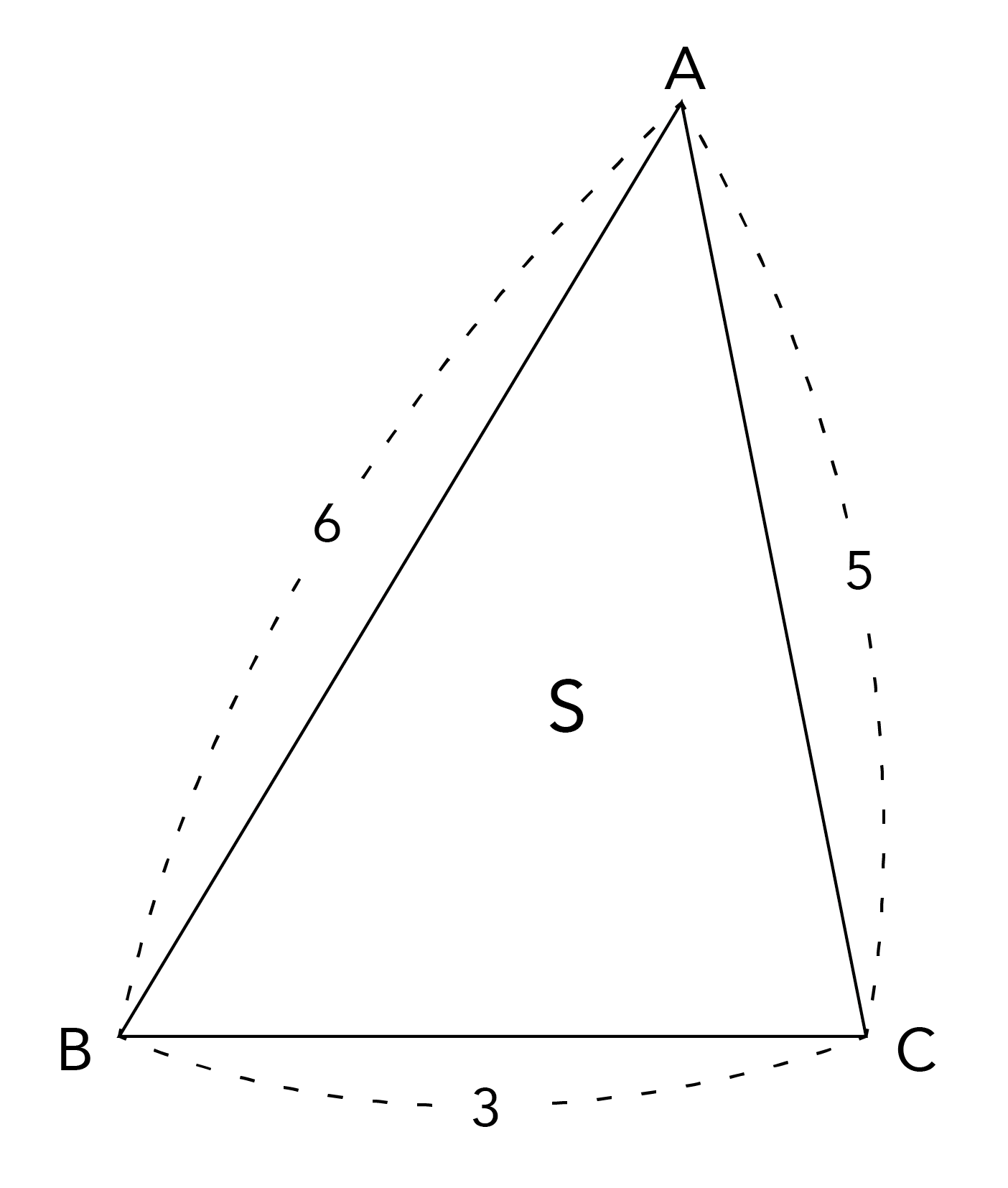


ヘロンの公式が一目でわかる 見やすい図で慶應生が解説 高校生向け受験応援メディア 受験のミカタ


ヘロンの公式の一般化


ヘロンの公式 Hero S Formula
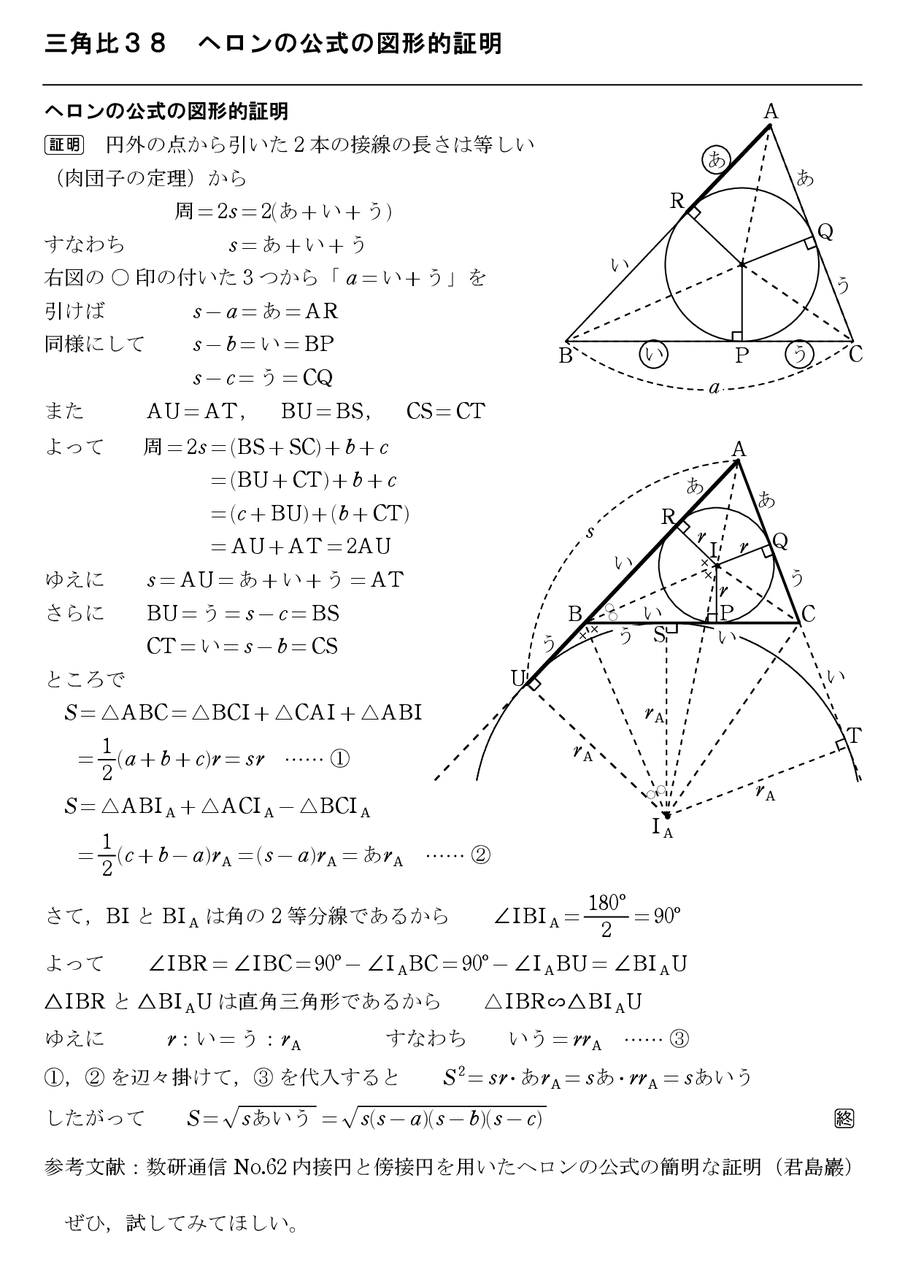


三角比38 ヘロンの公式の図形的証明 怜悧玲瓏 高校数学を天空から俯瞰する



ヘロンの公式の新着記事 アメーバブログ アメブロ



ヘロンの公式 Wikipedia



0 件のコメント:
コメントを投稿